들어가며
시간 복잡도, 알고리즘 복잡도 계산이 왜 필요할까?
시간 복잡도
점근 표기법?
왜 Big-O 표기법을 사용할까?
Big-O 표기법
# 들어가며
효율성 분석을 할 때 알고리즘 복잡도를 사용하여 검사를 합니다.
알고리즘 복잡도의 종류에는 시간 복잡도와 공간 복잡도가 있습니다.
그중 시간 복잡도에 대해 알아보겠습니다.
알고리즘 분석
- 정확성 분석
설계한 알고리즘을 다양한 수학적 기법을 사용하여 이론적으로 증명하거나 다양한 입력 상황을 가정하여 테스트 데이터를 통해 정확한 결과가 생성되었는지를 분석
- 효율성 분석
알고리즘 복잡도를 사용하여 효율적인 알고리즘인지를 분석
# 시간 복잡도, 알고리즘 복잡도 계산이 왜 필요할까?
알고리즘은 문제를 해결하는 방법, 절차입니다.
문제를 해결하는 방법은 여러 가지가 있고, 그중 어떤 것이 더 좋은지 판단하기 위해 복잡도를 사용합니다.
문제 해결을 가장 빠르게 하는 알고리즘이 좋다고 판단되어 시간 복잡도가 많이 사용됩니다.
# 시간 복잡도
시간 복잡도는 알고리즘의 수행 시간을 계산합니다.
테이블 방식을 이용해 알고리즘의 단계 수(연산 횟수)를 구합니다.
int sum(int n) { // 0
int sum = 0; // 1
for(int i = 1; i <= n; i++) // n+1
sum += i; // n
return sum; // 1
}
| 실행 여부(s/e) | 횟수(빈도) | 단계 수 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | n+1 | n+1 |
| 1 | n | n |
| 1 | 1 | 1 |
| 총 단계 수 | 2n+3 |
프로그램 단계 수
- 주석 : 0
- 선언문 : 0
→ 변수, 상수 정의(int, long, short, char, ... )
→ 사용자 데이터 타입 정의(class, struct, union, template)
→ 접근 결정(private, public, protected, friend)
→ 함수 타입 결정(void, virtual)
- 산술식 및 지정문 : 1
- 스위치 명령문
→ switch()의 비용 = 의 비용
→ 각 조건의 비용 = 자기의 비용 + 앞서 나온 모든 조건의 비용
- if~else 문
→ , , 에 따라 각각 단계수가 할당
- 함수 호출
→ 값에 의한 전달 인자 포함하지 않을 경우 : 1
→ 값에 인한 전달 인자 포함할 경우 : 값 인자 크기의 합
→ 순환적인 경우 : 호출되는 함수의 지역 변수도 고려
- 메모리 관리 명령문 : 1(new, delete)
- 함수 명령문(function statements) : 0
→ 비용이 이미 호출문에 해당
- 분기 명령문 : 1(continue, break, goto, return)
출처: https://ssu-gongdoli.tistory.com/21
테이블 방식에서 실행 여부와 횟수의 기준은 코드 한 줄(행)로 잡습니다.
해당 줄이 수행되면 1, 아니면 0
횟수는 해당 줄의 빈도수를 적습니다.
아래 코드로 예시를 들면
float Rsum(float *a, const int n) // 1
{ // 2
if(n <= 0) // 3
{ // 4
return 0; // 5
} // 6
else // 7
{ // 8
return (Rsum(a,n-1) + a[n-1]); // 9
} // 10
} // 11
1. 함수를 호출할 때 수행한다고 체크하기 때문에 함수 명령문은 단계를 체크하지 않는다.
실행 여부 0, 횟수 0 → 0
3. n이 0일 때 return하므로 n이 0이 될 때까지 비교(수행)한다. (n이 0이면 1번 수행, n이 1이면 2번 수행)
실행 여부 1, 횟수 n+1 → n+1
5. n이 0일 때 한번 수행된다.
실행 여부 1, 횟수 1 → 1
9. n이 0이 아닐 때마다 수행한다. 즉 n의 값만큼 수행
실행 여부 1, 횟수 n → n
0 + n+1 + 1 + n = 2n+2
단계 수는 2n+2가 된다.
# 점근 표기법?
점근 표기법(Asymptotic Notation)은 어떤 함수의 증가율을 다른 함수와의 비교로 표현하는 방법입니다.
시간 복잡도를 표기할 때 점근 표기법이 사용됩니다.
앞서 테이블 방식을 이용하여 단계 수를 구하는 방법으로 수행 시간을 확인했습니다.
하지만 이 방법은 내용이 복잡해질수록 알고리즘의 성능을 파악하기 어렵습니다.
예를 들어 A 알고리즘은 1, B 알고리즘은 2n+2, C 알고리즘은 2n² 일 때
A 알고리즘의 성능이 가장 좋다는 것을 알 수 있지만
수행 시간이 n²+4nlogn³+8n 과 2n²+3n 은 어떤 것이 더 좋은지 파악하기 어렵습니다.
그래서 점근 표기법을 사용하여 시간 복잡도를 표기합니다.
# 왜 Big-O 표기법을 사용할까?
점근 표기법의 종류에는 O(빅 오), Θ(세타), Ω(오메가) 등이 있습니다.
오메가 표기법은 최선의 수행 시간,
세타 표기법은 평균 수행 시간,
빅오 표기법은 최악의 수행 시간을 나타냅니다.
시간 복잡도에서 왜 빅오 표기법을 사용할까?
회사에 출근하기 위해 출근하는데 걸리는 시간을 생각한다고 가정하면
오메가는 최선, 지하철 기다리는 시간도 없고 신호등도 막히지 않을 때 30분 소요
세타는 최선과 최악의 중간(평균), 평균적으로 출근할 때 35분 소요
빅오는 최악, 지하철 대기시간 버스 막히는 시간까지 모두 포함시켜서 40분 소요
빅오 방법으로 출근해야 지각하지 않고 출근할 수 있습니다.
알고리즘의 효율성은 최악의 상황을 생각해야하기 때문에 빅오 표기법을 사용합니다.
# Big-O 표기법
빅오 표기법은 실제 수행 시간이 아닌 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 것이 목표입니다.
그래서 영향을 제일 많이 끼치는 가장 높은 항을 제외한 나머지를 제거(계수 포함)하고, 상수(숫자)는 모두 1이 됩니다.
(프로그래밍에서 시간 복잡도는 반복문의 영향을 가장 많이 받아서 반복문의 구성이 중요합니다.)
빅오 표기법의 종류
- O(1): constant
입력 데이터의 크기와 상관없이 일정한 시간이 걸리는 알고리즘

F(n){
return (n[0] == 0) ? true : false;
}
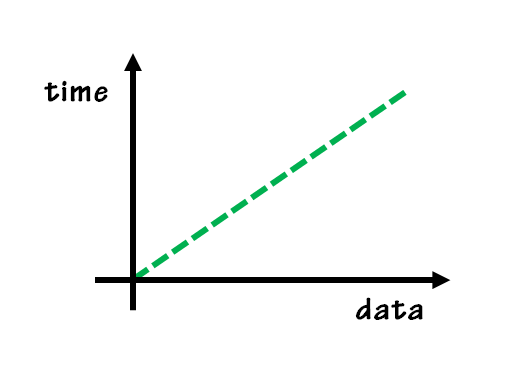
- O(n): linear
입력 데이터의 크기에 비례해서 처리 시간이 걸리는 알고리즘
F(n){
for(let i=0; i<n; i++){
console.log(i);
}
}
- O(n²): quadratic
입력 데이터가 커질수록 처리 시간이 증가하는 알고리즘

F(n){
for(let i=0; i<n; i++){
for(let j=0; j<n; j++){
console.log(i+j);
}
}
}
- O(n³): polynomial / cublic
입력 데이커가 커질수록 급격하게 처리 시간이 증가하는 알고리즘

F(n){
for(let i=0; i<n; i++){
for(let j=0; j<n; j++){
for(let k=0; k<n; k++){
console.log(i+j+k);
}
}
}
}
- O(2ⁿ): exponential
급격하게 처리 시간이 증가하는 '지수적 증가' 알고리즘
ex) 피보나치 Fibonacci
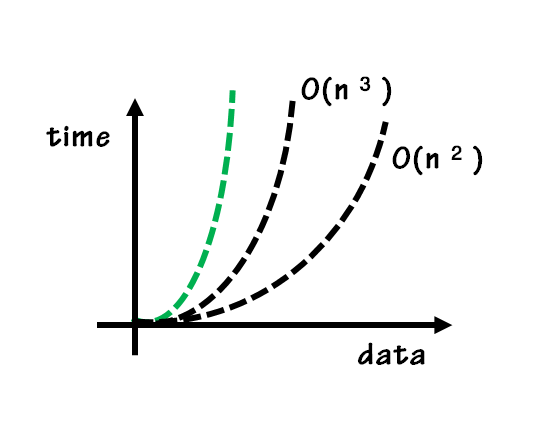
- O(log n)
문제 해결에 필요한 과정들이 연산마다 특정 요인에 의해 줄어드는 알고리즘
(데이터가 증가해도 성능이 크게 차이나지 않음)
ex) 이진탐색 binary search

F(k, arr, s, e){ //s는 시작(0번째), e는 마지막
if(s>e) return -1;
m = (s+e) / 2;
if(arr[m] == k) return m;
else if(arr[m]>k) return F(k,arr,s,m-1);
else return F(k, arr, m+1, e);
}
O(1): 상수형 constant
O(n): 선형 linear
O(n²): 2차형 quadratic
O(n³): 3차형 polynomial / cublic
O(2ⁿ): 지수형 exponential
O(log n): 로그형
이외에도 O(nlogn), O(n!) 등이 있습니다.
O(n log n): 로그선형
O(n!): 팩토리얼형 factorial

입력에 연산 시간
O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(n³) < O(2ⁿ) < O(n!)
(log n = log₂n)
예시
1부터 n까지 합을 구하는 알고리즘
1.
// 더하는 과정을 n번 반복: O(n)
F(n){
let total = 0;
for(let i=1; i<=n){
total += i;
}
return total;
}
2.
// 반복문 없이 n(n+1)/2 공식을 사용해 한 줄로 정리: O(1)
F(n){
return n(n+1)/2;
}
1번: O(n) 2번: O(1)
→ 2번이 1번보다 좋은 알고리즘이라고 할 수 있습니다.
